【鷹揚】日常生活で役立つ会計【アルバイトW】

こんにちは！「日本の資格・検定」編集部、大学生アルバイトWです！

〈ここまでのあらすじ〉
これまで数々の投稿記事を執筆してきたアルバイトW。
今まで取得した資格・検定の知識を活用し、含蓄に富む記事を書いてきたと思っていたが、
2022年12月のテーマ記事で振り返ってみると、知識が活かされていないことが判明。
合格に至るまでの血反吐を吐いた日々に報いるため、新たな記事の執筆に挑むのであった———

というわけで、
今回の記事では私が日商簿記1級の勉強を通じて身に付けた知識をご紹介したいと思います！

ですが、ただ知識をひけらかすだけでは芸がない、と思いましたので、

日常生活で起きた問題に対して簿記・会計の知識をどのように適用できるか
そして、その知識の簡単な解説をする

という構成になっております。

この記事を通じて、会計に触れたことのない方が、
少しでも会計に興味を持っていただけたら幸いです！
会計上級者の方は、生暖かい目でご覧ください・・・

※この記事に登場する商品の価格などは、計算の簡単化のため実際とは異なる場合があります。

こちらも要チェック！
〇12月のテーマ記事「2022年の資格・検定総まとめ」
〇11月のテーマ記事「資格・検定を活かせたエピソード」
〇個人的 就活に役立った資格・検定

​CASE1 : 一括払い、それとも分割払い？

太郎さんはクリスマスプレゼントとして、
最新モデルの iPad Pro をクレジットカードで購入することを検討しています。

しかし、円安や半導体不足などの種々の要因により、
iPad Pro の価格はとても高くなっているため、一括払いすることを躊躇しています。

かといって分割払いは、手数料や金利が掛かるため、
損をしてしまうのではないかとの印象を持っています。

iPad Pro の値段は12万円です。
太郎さんは①一括払い、もしくは②12回の分割払いを選択できることとし、
分割払いでは1回の支払あたり500円の手数料が掛かるものとします。
また、分割払いで利息は発生しないこととします。

太郎さんは一括払いと分割払い、どちらを選ぶべきなのでしょうか？

まず、総支払額を求めてみましょう。

①一括払いの場合：120,000 × 1 = 120,000円
②分割払いの場合：(120,000 / 12 + 500) × 12 = 10,500 × 12 = 126,000円

となるため、
太郎さんが思っている通り、分割払いの方が総支払額が6,000円高くなっています。

それでは、一括払いにすべきなのでしょうか？

ここで、二つの支払方法で決済のタイミングが違うことを考えてみましょう。
太郎さんはクリスマスプレゼントを購入しようとしているので、

①一括払いの場合：12月に120,000円支払い
②分割払いの場合：12月に10,500円、1月に10,500円、・・・、11月に10,500円支払い

となります。そのため、12月末時点における支払額は

①一括払いの場合：120,000円
②分割払いの場合：10,500円

となります。

ところで、12月25日はクリスマスであると同時に、
日本の重賞レースのひとつである有馬記念が開かれる日です。

太郎さんは、またの名を「生涯収支プラス1億円君」といい、
競馬について並外れた知識を持っているため、
馬券の購入額の2倍、払戻金を得ることができます。

つまり、馬券の購入額分利益を得ることができます。

12万円のうち、太郎さんが支払を先送りにした額(109,500円)だけ
有馬記念で馬券を購入できることを考慮して、1年間の純支払額を求めると

①一括払いの場合：120,000円
②分割払いの場合：126,000 - 109,500 = 16,500円

となるため、太郎さんは分割払いを選択することで、
120,000 - 16,500 = 103,500円だけ得することができるとわかります。

この設例で用いた会計知識は【機会費用】です。
日商簿記では、1級の原価計算の科目で登場します。
※この概念は会計だけでなく、経済学などにおいても出てきます。

機会費用とは、二つの選択肢がある状況で、
一方の選択をした場合に ”失われる” もう一方の選択肢における利益のことです。

上の例では、一括払いを選択した場合に得ることができない、
分割払いの場合における有馬記念での利益109,500円が機会費用にあたります。

他の機会費用の例としては、高卒で働く、もしくは大卒で働くという選択肢がある場合に、
大卒で働く場合に得ることができない、「大学4年間分の賃金」などがあります。

機会費用まで含めて比較することで、意思決定において正しい判断ができるようになります。

​CASE2 : 定期券を購入すべき？

4月から大学生になる花子さんは、
自宅がある品川駅から、大学がある渋谷駅までの
通学定期券を購入すべきかどうか検討しています。

品川ー渋谷間の電車の運賃は、片道370円です。
花子さんの大学は週4回の授業が15週(4か月)あります。
調べたところ、通学定期券は4か月で37,000円でした。

花子さんは通学定期券を購入すべきなのでしょうか？

まず、通学定期券の元を取るためには、何日通学すればよいのか求めてみましょう。

品川駅ー渋谷駅間の運賃は、往復で 370 × 2 = 740円なので、

37,000 / 740 = 50日

通学することで元を取ることができます。

全ての授業に出席する場合、4 × 15 = 60日大学に通学することになるため、
無事に元を取ることができそうです。

花子さんは、4月から始まるキャンパスライフに胸を躍らせながらみどりの窓口に赴き、
定期券を購入したそうです。

5月某日、花子さんは同じ大学に通っている高校時代の先輩から、あることを聞きました。

曰く、授業は5回までなら休んでも単位は認定される、と。

ゴールデンウイークを怠惰に過ごし、
すっかり学業へのモチベーションを失った花子さんにとっては願ってもない話です。

花子さんは計画的に出席日数を調整し、結局 4 × 10 = 40日大学に通学して夏休みを迎えました。

定期券の元を取るために必要な出席日数は50日でしたから、
花子さんは定期券を買うべきではなかった、と後悔することになったとさ。

この設例で用いた会計知識は【損益分岐点】です。
日商簿記では2級の工業簿記の分野で登場します。

損益分岐点とは、
収益と費用が等しくなるような販売数量もしくは売上高(販売数量 × 価格)を指し、
販売数量が損益分岐点を超えれば黒字、下回れば赤字となります。

概念上、費用は
①販売数量が増えるにつれて増加するような費用(変動費)
②販売数量に関わらず一定の費用(固定費)
の2種類に分類されます。

商品を1個販売することで得られる収益、すなわち価格と商品1個分の変動費の差が
商品を1個販売することで得られる利益であり、
これを限界利益と呼びます。

※限界利益の「限界」はmarginal という英語の訳で、
日常生活で使う”限界”とは異なる意味です。
経済学を勉強していると、限界○○という用語がたくさん出現します。

固定費を限界利益で割ることにより、
固定費を賄うためには何個商品を販売すれば良いか、
を計算することができ、これが損益分岐点です。

簿記のテキストなどでは、
損益分岐点の求め方の公式として次のような式を紹介していますが、
その原理は上述した通りです。

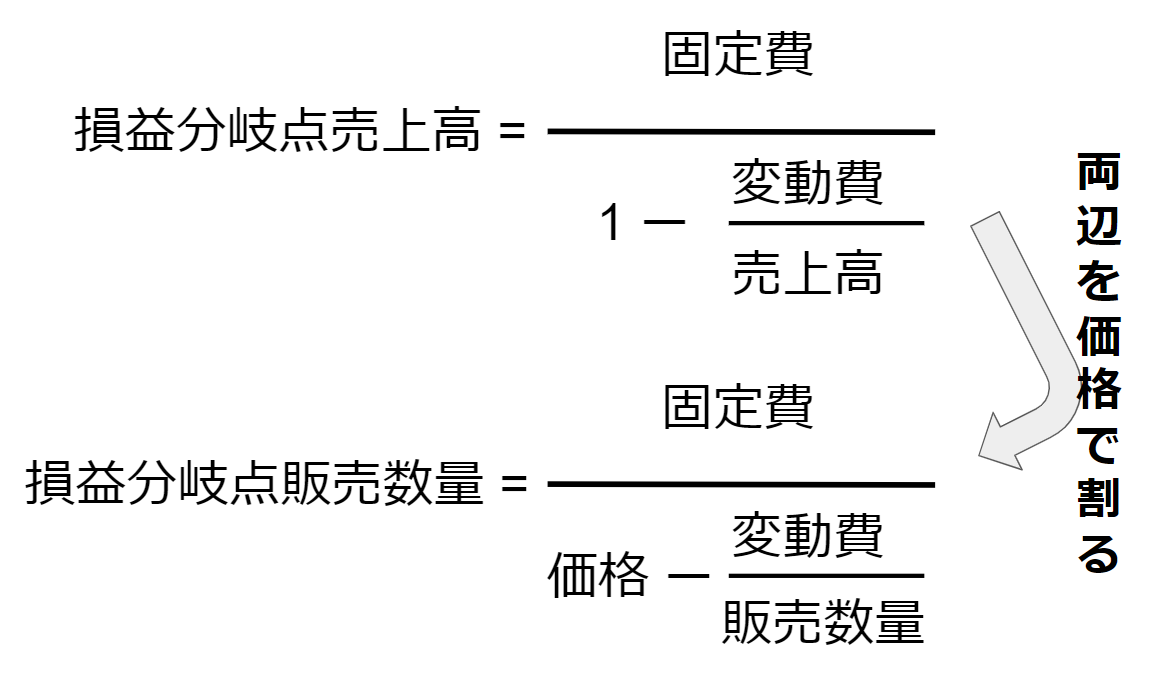
上の例では単純化のために変動費 = 0 としたうえで、
37000 / 740 = 50 という計算で損益分岐点を求めています。
もっとも、商品を販売云々という設定ではないのですが。

CASE3 : どの中古車がお得？

キャサリンさんは車検の更新のタイミングで車を買い替えることを検討しています。

中古車のディーラーを尋ね、希望の車種を伝えると
「そこに3台のプリウスがあるじゃろ」と以下の車を紹介されました。

A：15年落ち　走行距離130,000km　100万円　サーモテクトライムグリーン色
B：10年落ち　走行距離100,000km　150万円　エモーショナルレッド色
C：5年落ち　走行距離70,000km　200万円　ダークブルーマイカメタリック色

どの車を選べば良いのか困り、ディーラーに尋ねてみたところ、
「プリウスは全世界で151台しか生産されていない」などと
訳のわからないことしか言わないため、独力で考えることにしました。

キャサリンさんがこれまで乗っていた車は20年前に新品で購入したものです。
先月走行距離が200,000kmに達してから、頻繁に故障するようになったため、
20年落ち、走行距離200,000kmを寿命の目安として考えています。

新品のプリウスの価格は250万円ですが、当然この店には売っていません。

果たして、キャサリンさんはどの中古車を購入すべきなのでしょうか？

キャサリンさんは年式・走行距離を考慮してそれぞれの中古車の価値を算定し、
よりお買い得な車を選ぼうとしています。

年式から価値を算定するにあたって、
20年の寿命を残す新車が250万円であることを鑑みると、

A：15年落ち → 5 / 20 × 250 = 62.5万円
B：10年落ち → 10 / 20 × 250 = 125万円
C：5年落ち → 15 / 20 × 250 = 187.5万円

が妥当な価値であるように思われ、

A：100万円 → 62.5万円より37.5万円高い
B：150万円 → 125万円より25万円高い
C：200万円 → 187.5万円より12.5万円高い

と計算できるため、Cの車がお買い得だと判断できます。

今度は走行距離から価値を算定してみましょう。
200,000km走行できる新車が250万円であることを鑑みると、

A：残存走行距離70,000km → 70,000 / 200,000 × 250 = 87.5万円
B：残存走行距離100,000km → 100,000 / 200,000 × 250 = 125万円
C：残存走行距離130,000km → 130,000 / 200,000 × 250 = 162.5万円

が妥当な価値であるように思われ、

A：100万円→87.5万円より12.5万円高い
B：150万円→125万円より25万円高い
C：200万円→162.5万円より37.5万円高い

と計算できるため、Aの車がお買い得だと判断できます。

なんということでしょう。
年式を基準にするか、走行距離を基準にするかによって、
車のお得度が全く変わってしまいました。

ここまで考えたところで、キャサリンさんは朝のめざまし占いで、
ラッキーカラーは赤色、と言われていたことを思い出し、
エモーショナルレッド色であるBの車を購入することに決めたそうです。

この設例で用いた会計知識は【減価償却】です。
日商簿記では3級から登場します。

会計には、
収益とそれを生むために要した費用を対応させて決算書に表示しよう、
という原則があります。
そのため、会計期間をまたぐような費用は
見越・繰延処理(前払・未収など)を行って収益と対応させます。

しかし、費用の中には、
どの期の収益と対応している、というのが一概には言えないようなものがあり、
その最たる例が固定資産の費用計上です。

固定資産は収益を生むために役立っているはずですが、
1年でなくなってしまうわけではないので
複数期にわたって費用計上すべきだと考えられています。

そこで登場するのが減価償却という処理なのです。

減価償却の仕方は複数存在していて、
継続して適用しさえすればどの方法を用いても問題ありません。

例えば、毎年一定額を費用計上する「定額法」や
固定資産を購入してすぐの期間に多めに費用計上する「定率法」、
固定資産を使用した時間などの指標に基づいて費用計上する「生産高比例法」
などが有名どころです。

上の例では、年式での価値算定は定額法を、
走行距離での価値算定は生産高比例法を用いています。

まとめ

以上、会計知識の活用事例を3つご紹介してまいりましたがいかがでしたか？

簿記は「役に立つ資格・検定」とよく言われますが、
経理などの決算書に関わる仕事以外で
役に立っていることを実感するタイミングって
意外と少ないのではないかと思います。

今回の3つの設例は、
(その細かい妥当性はさておき)日常生活でもありえそうな意思決定問題を取り上げています。

それらの問題に対処するうえで、
会計の観点からどのように考えられるかをご理解いただき、
少しでも会計に興味を持っていただけたなら幸いです。

〔担当：アルバイトW〕

【属性】大学生アルバイト
【好きな鳥類】ケープペンギン
【意気込み】読んだ方にクスリと笑っていただけるような記事を目指して頑張ります！